不偏分散は n-1 で割る理由

今回は統計学を学ぶ中で必ず疑問に思うであろう、不偏分散において $n-1$ で割る理由をまとめていきたいと思います。

標本分散と不偏分散の復習

標本分散と不偏分散は次のように定義されます。

確率変数列 $X_1,X_2,\cdots,X_n$ が得られとする。このとき標本分散 $S^2$ と不偏分散 $U^2$ は次のように定義される。

$$\begin{align*} \text{標本分散}\quad&S^2 = \frac{1}{n}\sum^{n}*{i=1}(X_i-\bar{X})^2\\ \text{不偏分散}\quad&U^2 = \frac{1}{n-1}\sum^{n}_{i=1}(X_i-\bar{X})^2 \end{align*}$$

これらの違いは見てわかる通り、$n$ で割るか $n-1$ で割るかの違いです。ではこれらの違いは何なのかと言うと、$n$ で割る方は不偏推定量ではなく、$n-1$ で割る方は不偏推定量であるという点です。念の為、不偏推定量の復習をしておくと、推定量の期待値が真のパラメータと一致する推定量のことを言います。

不偏分散が不偏推定量であることの証明

では不偏分散が本当に不偏推定量であるかどうかの証明を行います。

母平均 $\mu$、母分散 $\sigma^2$ の確率分布に従う確率変数 $X_1,\cdots,X_n$ を考えます。これを踏まえて、標本分散と不偏分散の式の共通している部分である偏差平方和 $\sum^{n}_{i=1}(\bar{X}-X)$ の期待値を求めてみましょう。

$$\begin{align*} E\left[\sum^{n}_{i=1}(X_i-\bar{X})^2\right] &= E\left[\sum^{n}_{i=1}\{(X_i-\mu)-(\bar{X}-\mu)\}^2\right]\\ &= E\left[\sum^{n}_{i=1}\{(X_i-\mu)^2-2(X_i-\mu)(\bar{X}-\mu)+(\bar{X}-\mu)^2\}\right]\\ &= E\left[\sum^{n}_{i=1}(X_i-\mu)^2-2(\bar{X}-\mu)\sum^{n}_{i=1}(X_i-\mu)+\sum^{n}_{i=1}(\bar{X}-\mu)^2\right]\\ &= E\left[\sum^{n}_{i=1}(X_i-\mu)^2-2(\bar{X}-\mu)\{n(\bar{X}-\mu)\}+n(\bar{X}-\mu)^2\right]\\ &= E\left[\sum^{n}_{i=1}(X_i-\mu)^2-2n(\bar{X}-\mu)^2+n(\bar{X}-\mu)^2\right]\\ &= E\left[\sum^{n}_{i=1}(X_i-\mu)^2-n(\bar{X}-\mu)^2\right]\\ &= E\left[\sum^{n}_{i=1}(X_i-\mu)^2\right]- nE\bigg[(\bar{X}-\mu)^2\bigg]\\ &= E\left[\sum^{n}_{i=1}(X_i-\mu)^2\right]- nE\left[\left\{\frac{1}{n}\sum^{n}_{i=1}({X_i}-\mu)\right\}^2\right]\\ &= n\sigma^2 - n\frac{n\sigma^2}{n^2}\\ &= n\sigma^2 - \sigma^2\\ &= (n-1)\sigma^2\\ \end{align*}$$

長くなりましたが、偏差平方和の期待値は $(n-1)\sigma^2$ となることがわかりました。これを踏まえて、不偏分散の期待値を求めてみましょう。

$$\begin{align*} E\left[\frac{1}{n-1}\sum^{n}_{i=1}(X_i-\bar{X})^2\right] &= \frac{1}{n-1}E\left[\sum^{n}_{i=1}(X_i-\bar{X})^2\right]\\ &= \frac{1}{n-1}(n-1)\sigma^2\\ &= \sigma^2 \end{align*}$$

不偏分散の期待値が母分散 $\sigma^2$ と一致しました。つまり、分散の推定量として不偏分散を用いれば、不偏推定量となるということです。逆に標本分散の期待値も求めてみましょう。

$$\begin{align*} E\left[\frac{1}{n}\sum^{n}_{i=1}(X_i-\bar{X})^2\right] &= \frac{1}{n-1}E\left[\sum^{n}_{i=1}(X_i-\bar{X})^2\right]\\ &= \frac{1}{n}(n-1)\sigma^2\\ &= (1-\frac{1}{n})\sigma^2\\ &= \sigma^2-\frac{1}{n}\sigma^2 \end{align*}$$

標本分散の期待値は母分散 $\sigma^2$ より $\frac{1}{n}\sigma^2$ 小さく母分散と一致しないことがわかりました。こうした理由から、母分散の推定を行う時は標本分散 $S^2$ ではなく不偏分散 $U^2$ を利用します。

標本分散と不偏分散の違いを可視化

理論的に標本分散と不偏分散の違いを説明しましたが、それだけではふーんで終わってしまうかもしれないので、その違いを可視化して終わりにしたいと思います。

下のグラフは各サンプルサイズにおいて分散 $10^2$ の正規分布に従う乱数を複数回発生させ、それぞれの標本分散、不偏分散の平均をプロットしたグラフです。（Pythonコードはグラフの下に載せています。） これを見ると、不偏分散は最初から100付近を動いているのたいして、標本分散はかなり母分散 $10^2$ とは離れた値を出しています。サンプルサイズが増えてきても標本分散は母分散より小さい値を取っています。

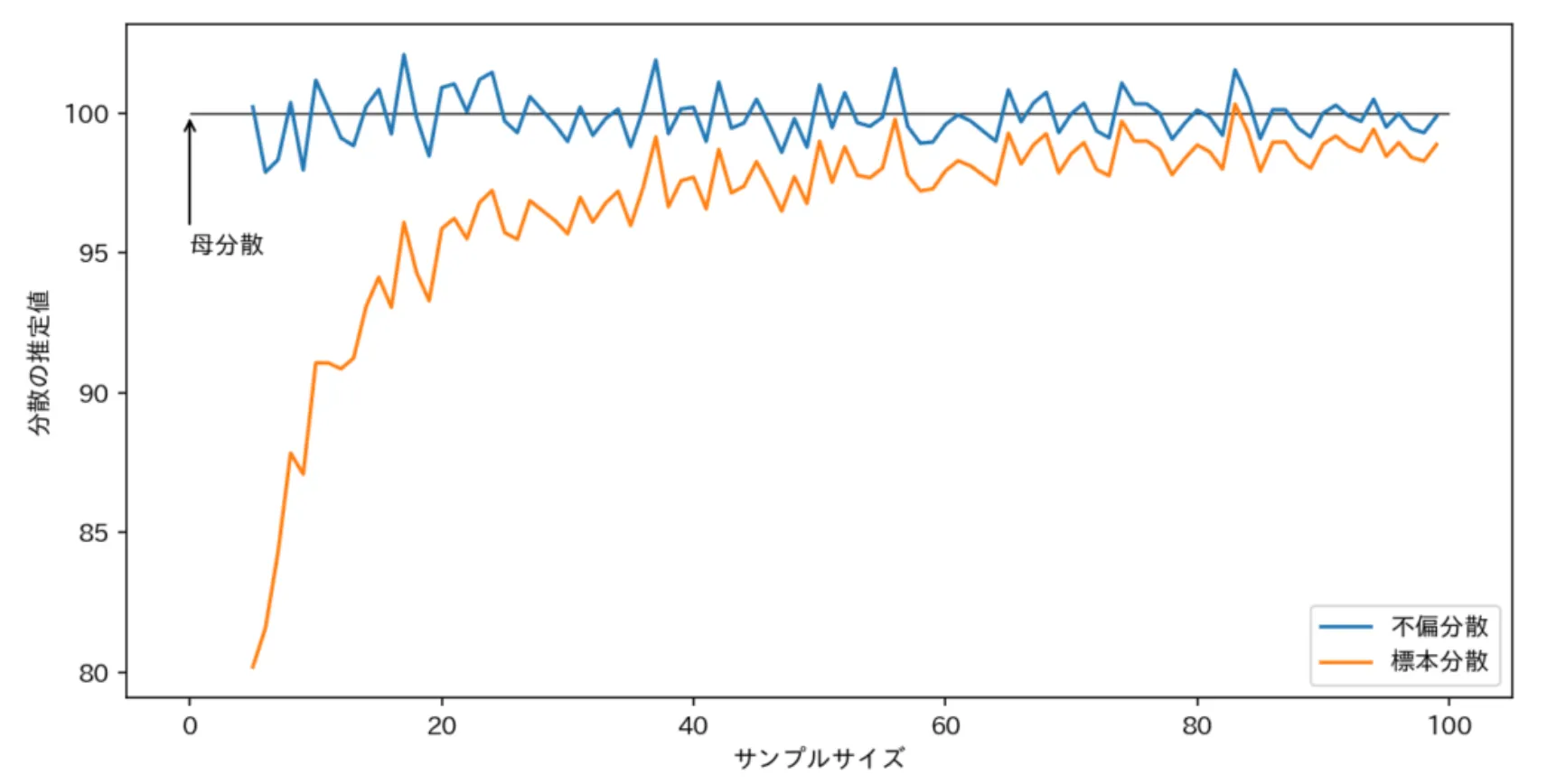
[Pythonコード]

あまり綺麗なコードではないと思いますが、ご容赦ください。

import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib

def cal*variance(sample_size, loc, scale):
sample = np.array([np.random.normal(loc, scale) for * in range(sample_size)])
biased_sample_variance = sample.var(ddof=0)
unbiased_variance = sample.var(ddof=1)
return biased_sample_variance, unbiased_variance

fig = plt.figure(figsize=(10,5), dpi=150)
n = 100
scale = 10
bsv*mean_list = []
ubv_mean_list = []
sample_size_list = range(5, n)
for sample_size in sample_size_list:
bsv_list = []
ubv_list = []
for * in range(1000):
bsv, ubv = cal_variance(sample_size, 0, scale)
bsv_list.append(bsv)
ubv_list.append(ubv)
bsv_mean_list.append(np.mean(bsv_list))
ubv_mean_list.append(np.mean(ubv_list))

plt.hlines(y=scale\*\*2, xmin=0, xmax=n, color='black', linewidth=0.7)
plt.plot(sample_size_list, ubv_mean_list, label='不偏分散')
plt.plot(sample_size_list, bsv_mean_list, label='標本分散')
plt.xlabel('サンプルサイズ')
plt.ylabel('分散の推定値')

arrow_props = dict(arrowstyle = "->", color = "black",
connectionstyle = "angle, angleA = 0, angleB = 90")

plt.annotate(text='母分散',
xy=(0,scale**2),
xytext=(0, scale**2 - 1/20 \* scale\*\*2),
arrowprops=arrow_props)
plt.legend()

まとめ

今回の記事をまとめると偏差平方和の期待値が

$$\begin{align*} E\left[\sum^{n}_{i=1}(X_i-\bar{X})^2\right] = (n-1)\sigma^2 \end{align*}$$

となるため、分散の不偏推定量は不偏分散の式になると言うことでしたね。

「不偏分散はなぜ $n-1$ で割るのか？」というテーマで、理論的な証明やグラフを用いて、標本分散と不偏分散の違いの説明しました。証明を覚えている必要はないと思いますが、なぜ $n-1$ で割るのかと言う理由を知っておいて損はないと思います。今回は以上です。