主成分分析（PCA）の基本的な考え方

主成分分析とは

主成分分析（PCA：Principal Component Analysis）とは、観測データに対してそのデータの特徴を要約するような主成分軸を決定し、その軸に観測データを射影した点を主成分とする変換を行う手法です。また、主成分分析は主に次元削減を行うために用いられる手法です。

概要の視覚的理解

主成分分析を視覚的に理解するために次のような2次元データを用意しました。

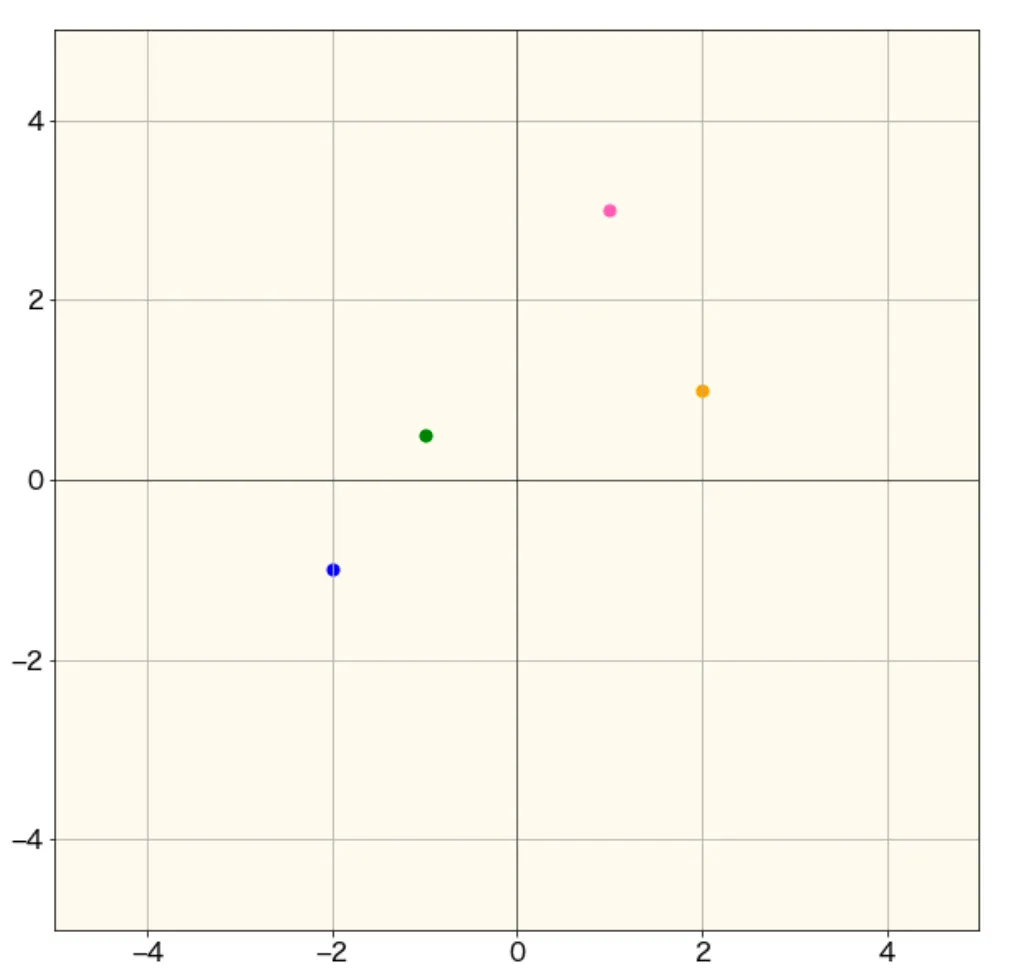
このデータに対して、射影ベクトル（軸）を1つ考えると次のようになります。どのように射影ベクトルを決めるかというと、射影ベクトルで射影した点（軸に対する垂線との交点）の分散が最大となるように射影ベクトルを決めます（※具体的な求め方や理由は導出のセクションで述べます）。そうして決定した射影ベクトルを主成分といい、データの特徴を要約した新たなデータを生成します。

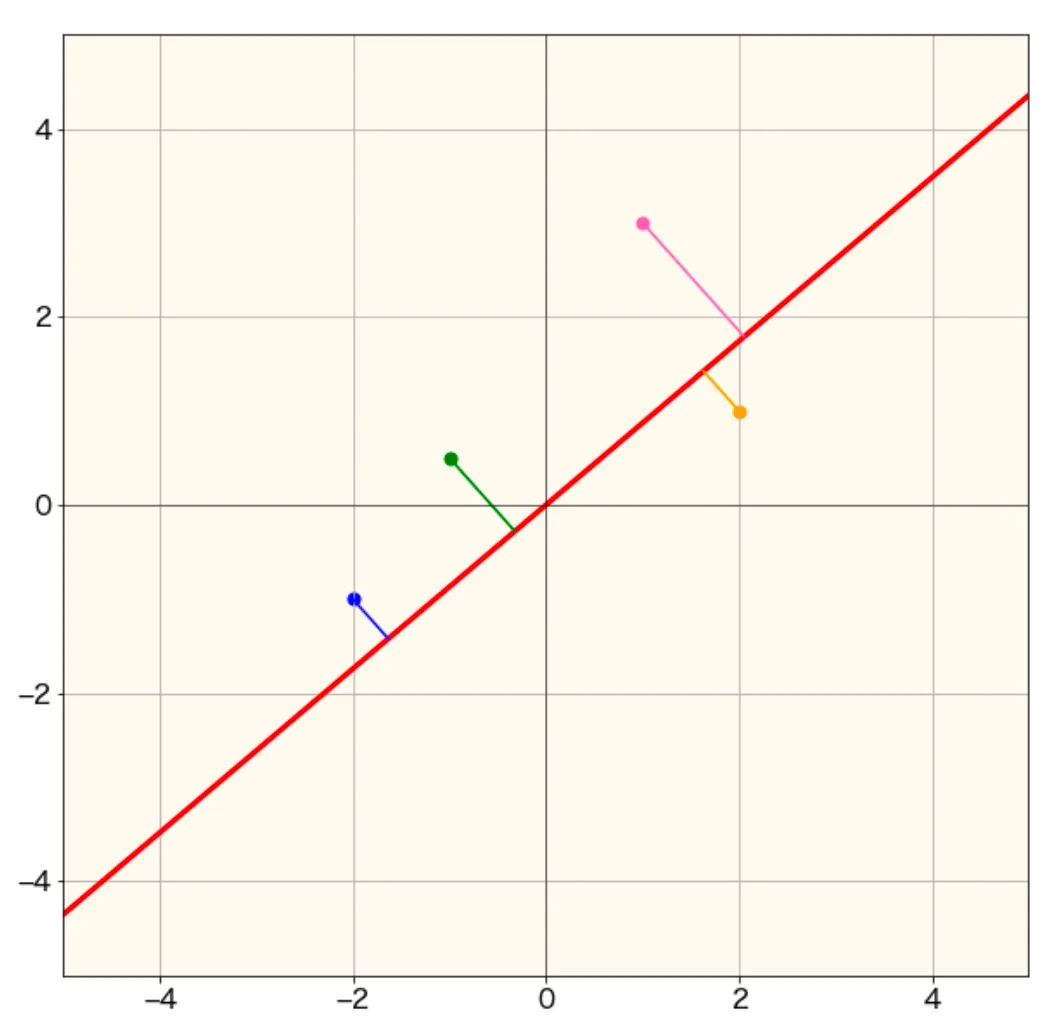
そして、射影した点の分散が最大となる軸を考えたときに一番最初に考えられる主成分（射影ベクトル）を第一主成分といいます。そこから第二主成分、第三主成分・・と、元のデータと同じ次元だけ主成分を考えることができます。その中で必要な数だけ主成分を選択し、次元削減を行います。第何主成分まで利用するかの判断に累積寄与率というものを参考にするので、それについても後半に説明しようと思います。

ちなみに上のデータは2次元データなので、第二主成分まで考えることができます。実際に第二主成分を描いてみると次のようになります。

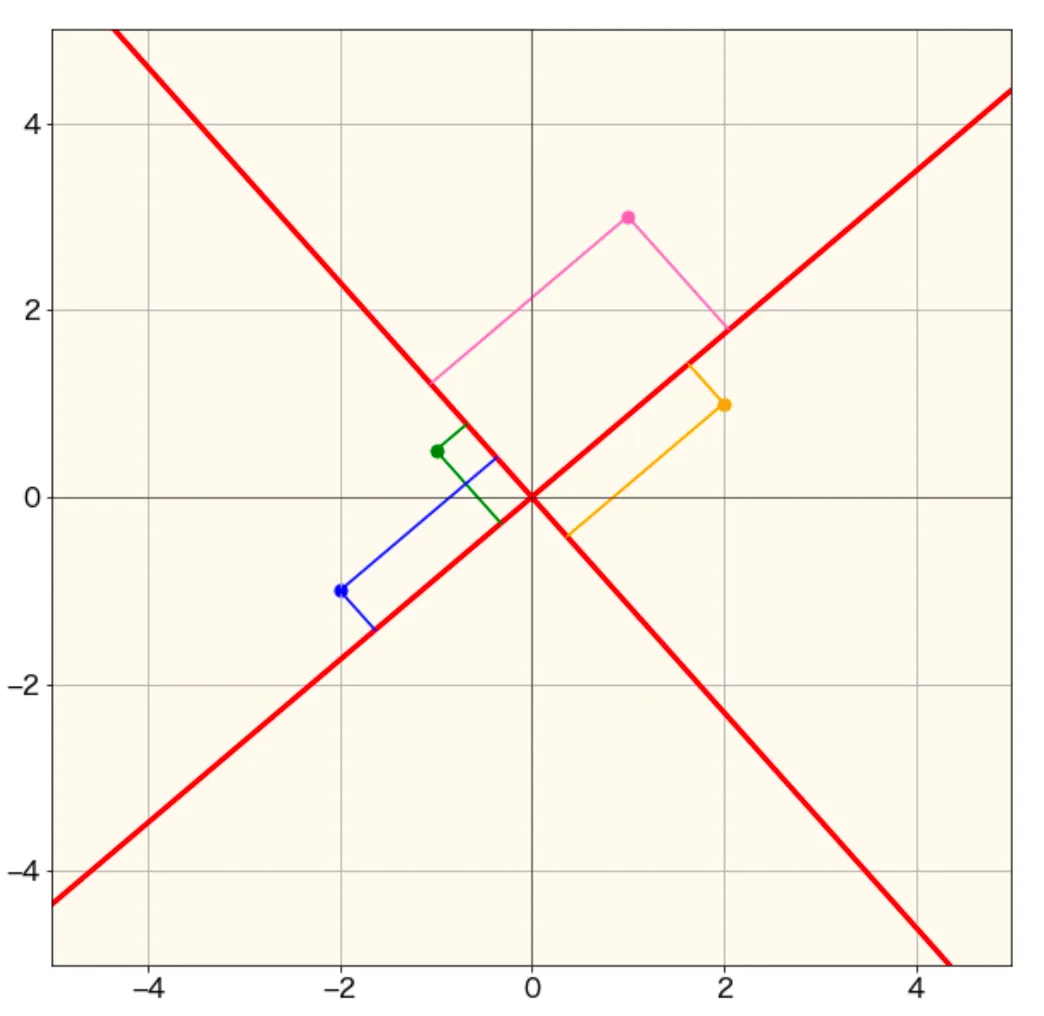
第一主成分と直交する第二主成分が追加されました。このように、主成分分析では他の主成分と直交するように次々と主成分を決めていきます。

概要の数式的理解

さきほどは、主成分分析について視覚的に説明しましたが、今度は数式を用いて概要を説明したいと思います。

では次のような国語と数学と英語のデータが得られたとします。

$$X = \left( \begin{array}{ccc} \text{国語}& \text{数学} & \text{英語}\\\hline x_{11}&x_{12}&x_{13}\\ x_{21}&x_{22}&x_{23}\\ &\vdots&\\ x_{n1}&x_{n2}&x_{n3}\\ \end{array}\right) =\left( \begin{array}{ccc} \bm{x}_1^T\\ \bm{x}_2^T\\ \vdots\\ \bm{x}_n^T\\ \end{array}\right)$$

このデータの $i$ 行目 $\bm{x}_i$ を射影ベクトル（主成分）$\bm{w}_1\in\mathbb{R}^3$ によって射影することは次のような一次結合の式で表現されます。

$${y}_{i1} = \bm{w}_1^T\bm{x}_i = w_{11}x_{i1}+ w_{12}x_{i2}+ w_{13}x_{i3}$$

このとき、$y_{1i}$ は主成分得点といいます。これを行列とベクトルを用いて表現すると、

$$X\bm{w}_1= \left( \begin{array}{ccc} w_{11}x_{11}+ w_{12}x_{12}+ w_{13}x_{i3}\\ w_{11}x_{21}+ w_{12}x_{22}+ w_{13}x_{23}\\ \vdots\\ w_{11}x_{n1}+ w_{12}x_{n2}+ w_{13}x_{n3}\\ \end{array} \right)= \left( \begin{array}{ccc} \bm{w}_1^T\bm{x}_1\\ \bm{w}_1^T\bm{x}_2\\ \vdots\\ \bm{w}_1^T\bm{x}_n\\ \end{array} \right)= \left( \begin{array}{ccc} y_{11}\\ y_{12}\\ \vdots\\ y_{1n}\\ \end{array} \right)$$

つまり、主成分得点は観測データの行列と主成分の積で表され、各要素をみると、1行分のデータ（ベクトル）と主成分（射影ベクトル）の内積によって算出されています。

ではどのように主成分（射影ベクトル）を求めるのかというと固有値・固有ベクトル問題を解くことで求めることができます。

主成分分析と固有値・固有ベクトル問題の関係については次のようになります。

$n$ 行 $p$ 列の観測データの行列 $X$ の分散共分散行列を $S$ としたとき、$S$ の固有値を次のように大きい方から並べます。

$$\lambda_1 \ge \lambda_2 \ge \cdots \ge \lambda_p$$

このとき、$\lambda_1$ に対応する固有ベクトルが第一主成分であり、同様にして$\lambda_2$ に対応する固有ベクトルが第二主成分となります。

つまり、主成分分析はデータの分散共分散行列の固有値・固有ベクトルを求めることで行うことができます。主成分分析の概要の数式的理解はここまでです。

「なんで？？」と思う方のために次のところからなぜ固有値・固有ベクトルの問題になるのかを「第一主成分の導出」、「第 $p$ 主成分の導出」より説明したいと思います。また「累積寄与率」については最後に説明します。

主成分分析を詳しく説明

射影軸の決め方

先ほど主成分の決め方として「射影した点の分散が最大になる射影ベクトル」と言いましたが、いきなり分散が最大になると言われてもピンと来ないと思います。ですので、改めて説明を加えたいと思います。下の図は冒頭でも見た図ですが、情報量の記述を追加しました。

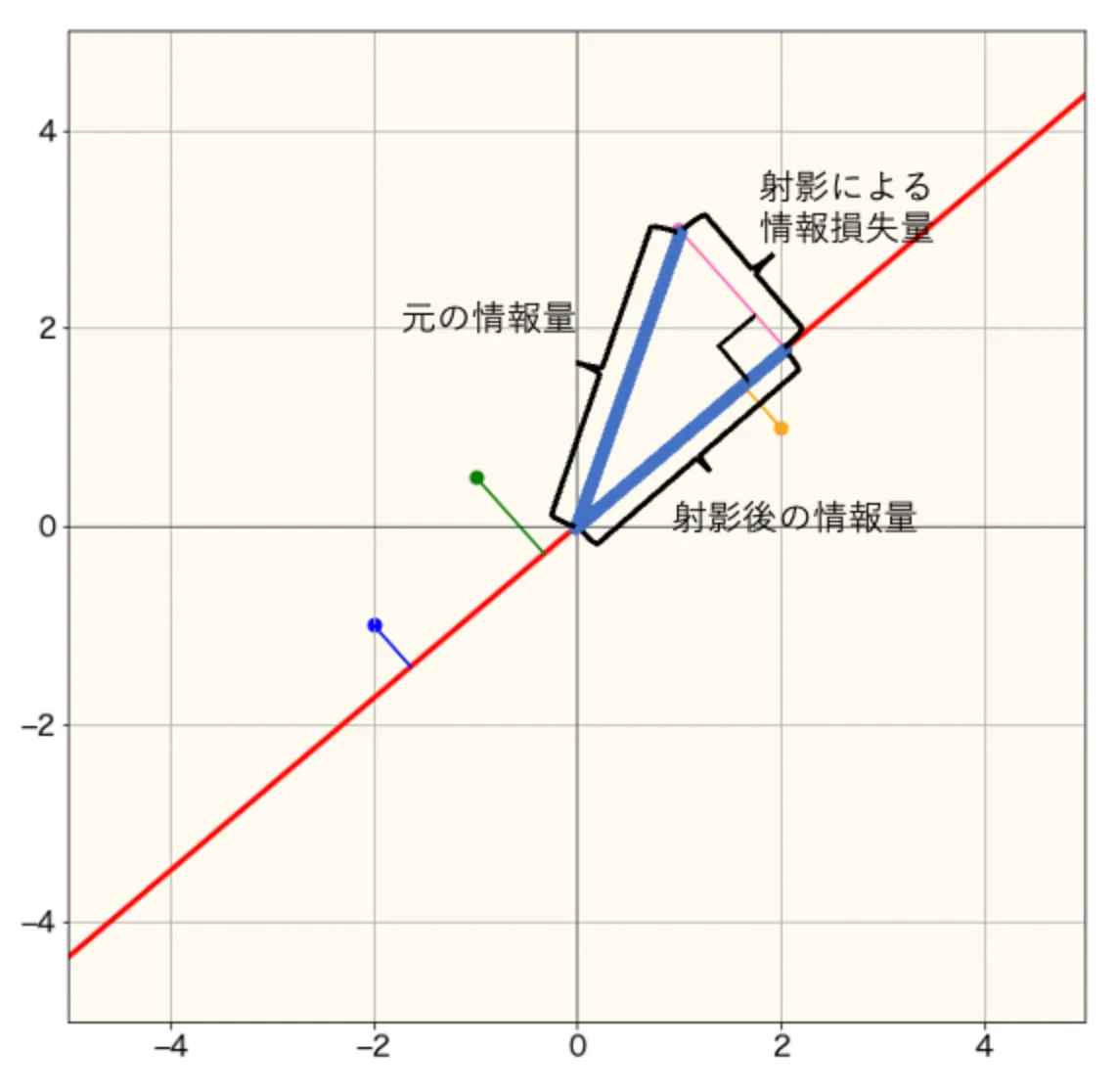
この図の直角三角形に注目してください。斜辺が元の情報量、射影軸に対して垂直な辺が射影による情報損失量、残りの辺が射影後の情報量です。軸を決めるときはこの損失情報量を最小化することを考えますが、このことは射影後の情報量を最大化することと同値であることがわかると思います。そして、射影後の情報量を最大化することが射影後のデータの分散を最大化することと同値であることが上で示した図からわかります。

このことを踏まえて最初に第一主成分の導出を解説しますが、その前に、行列とベクトルの定義をしておきます。次のように $p$ 次元データの行列 $X$、第 $j$ 主成分 $\mathbb{w}_j$、各列の平均を要素に持つ平均ベクトル $\bar{\mathbb{x}}$ を定義します。

$$X = \left( \begin{array}{cccc} x_{11}&x_{12}&\cdots&x_{1p}\\ x_{21}&x_{22}&\cdots&x_{2p}\\ \vdots&\vdots&\ddots&\vdots\\ x_{n1}&x_{n2}&\cdots&x_{np}\\ \end{array} \right)= \left( \begin{array}{ccc} \bm{x}_1^T\\ \bm{x}_2^T\\ \vdots\\ \bm{x}_n^T\\ \end{array} \right),\quad \bm{w}_j = \left( \begin{array}{ccc} w_{j1}\\ w_{j2}\\ \vdots\\ w_{jp}\\ \end{array} \right)$$ $$\bar{{\bm{x}}}^T = (\bar{{x}}_1, \bar{{x}}_2,\cdots, \bar{{x}}_p)$$

第一主成分の導出

それでは第一主成分の導出をしていきます。主成分は射影ベクトル $\bm{w}_j$ で射影した点の分散が最大になるような $\bm{w}_j$ に決めるということだったので、まずは射影した点の平均と分散を行列とベクトルを用いて表現していきましょう。

射影した点の平均は

$$\begin{align*} \frac{1}{n}\sum^{n}_{i=1}(w_1x_{i1} + w_2x_{i2} + \cdots + w_nx_{in}) &= \frac{1}{n}\sum^{p}_{j=1}w_{j1}\sum^{n}_{i=1}x_{ij}\\ &= \sum^{p}_{j=1}w_{j1}\left(\frac{1}{n}\sum^{n}_{i=1}x_{ij}\right)\\ &= \sum^{p}_{j=1}w_{j1}\bar{x}_{j}\\ &= \bm{w}_1^T\bar{\bm{x}} \end{align*}$$

となります。そして、射影した点の平均を用いて次のベクトルを定義します。

$$\begin{align*} \overline{{X}\bm{w}_1} = ( \bm{w}_1^T\bar{\bm{x}}, \bm{w}_1^T\bar{\bm{x}}, \cdots, \bm{w}_1^T\bar{\bm{x}} )^T= \left( \begin{array}{cccc} \bar{x}_1&\bar{x}_2&\cdots&\bar{x}_p\\ \bar{x}_1&\bar{x}_2&\cdots&\bar{x}_p\\ \vdots&\vdots&\ddots&\vdots\\ \bar{x}_1&\bar{x}_2&\cdots&\bar{x}_p\\ \end{array} \right)\bm{w}_1= \bar{X}\bm{w}_1 \end{align*}$$

すると、射影した点の分散は次のように表されます。

$$\begin{align*} J_1 &=\frac{1}{n-1}({X}\mathbb{w}\_1-\overline{{X}\mathbb{w}\_1})^T({X}\mathbb{w}\_1-\overline{{X}\mathbb{w}\_1})\\ &= \frac{1}{n-1}(X\bm{w}\_1 - \bar{X}\bm{w}\_1)^T(X\bm{w}\_1 - \bar{X}\bm{w}\_1)\\ &= \frac{1}{n-1}\left[(X - \bar{X})\bm{w}_1\right]^T(X - \bar{X})\bm{w}\_1\\ &= \frac{1}{n-1}\bm{w}\_1^T(X - \bar{X})^T(X - \bar{X})\bm{w}\_1\\ &= \bm{w}\_1^TS\bm{w}\_1 \end{align*}$$

このとき $S$ は $X$ の分散共分散行列です。よって、射影した点の分散は分散共分散行列と射影ベクトルの二次形式によってもとまることがわかりました。ここで、分散共分散行列 $S$ は実対称行列であるということが後ほど役に立つので頭の片隅に置いておいてください。

最終的には射影した点の分散を最大化することが目的でした。つまり、先ほどの軸に射影した点の分散 $J_1$ を最大化するような射影ベクトルを求めます。しかし、ここで1つ問題が出てきます。現状だと $\mathbb{w}\_1$ の要素の値を大きくすればするほど分散 $J_1$ は大きくなります。しかし、主成分分析では軸の方向さえ決まればいいわけです。そこで、次のような制約条件のもと最大化を行います。

[制約条件]

射影ベクトル $\mathbb{w}\_j$ は次の条件を満たすとする

$$||\bm{w}_j||_2 = \sqrt{w_{1j}^2 + w_{2j}^2 + \cdots + w_{nj}^2}=1$$

こうした制約条件のもと最大化を行う時はラグランジュの未定乗数法が利用できますね。

$$\begin{align*} J_1 - \lambda_1(\bm{w_1}^T\bm{w_1}-1) &= 0\\ \bm{w}_1^TS\bm{w}_1 - \lambda_1(\bm{w_1}^T\bm{w}_1-1) &= 0 \end{align*}$$

$\bm{w}\_1$ について微分して $0$ とおくと

$$\begin{align*} 2S\bm{w}_1 - 2\lambda_1\bm{w}_1 &= 0\\ S\bm{w}_1 &= \lambda_1\bm{w}_1 \end{align*}$$

これは観測データ $X$ の分散共分散行列 $S$ の固有値・固有ベクトル問題に他なりません。つまりラグランジュ乗数 $\lambda_1$ は固有方程式における $\lambda_1$ と同じ意味合いを持ちます。ここで、左から $\mathbb{w}\_1^T$ を掛けると

$$\begin{align*} \bm{w}_1^TS\bm{w}_1 &= \lambda_1\bm{w}_1^T\bm{w}_1\\ J_1 &= \lambda_1 \end{align*}$$

となります。このことから射影した点の分散は分散共分散行列 $S$ の固有値と一致することがわかります。そして、その固有値に対応する固有ベクトルが主成分になります。つまり、一番大きな固有値に対応する「固有ベクトル」が射影した点の分散を最大とする第一主成分軸になるということです。

第 $j$ 主成分の導出 $(j\ge2)$

次に第 $j$ 主成分の導出を行いますが、基本的には第一主成分と同じです。ただし、次のような前提条件及び制約条件のもと射影した後の点 $J_j$ の分散を最大化することを考えます。

[前提条件]

第 $(j-1)$ 主成分まで求まっており、$2\le j\le p$ としたとき

$$\begin{align*} S\bm{w}_j &= \lambda_j\bm{w}_j \end{align*}$$

が成り立つ。

[制約条件]

射影ベクトル $\bm{w}\_j$ は次の条件を満たすとする

$$||\bm{w}_j||_2 =1,\quad \bm{w}_i^T\bm{w}_j=\left\{ \begin{array}{cl} 1& (i=j)\\ 0& (i\not= j) \end{array} \right.$$

この制約条件のもと射影後の分散 $J_j$ の最大化をする。先と同様にラグランジュの未定乗数法を用いると

$$\begin{align*} J_j\: - \:\lambda_j(\bm{w}_j^T\bm{w}_j-1)\: - \sum^{j-1}_{k=1}\mu_k\bm{w}_j^T\bm{w}_k &= 0\\ \bm{w}_j^TS\bm{w}_j\: - \:\lambda_j(\bm{w}_j^T\bm{w}_j-1)\: - \sum^{j-1}_{k=1}\mu_k\bm{w}_j^T\bm{w}_k &= 0 \end{align*}$$

$\bm{w}\_j$ について微分して $0$ とおくと

$$\begin{align} 2S\bm{w}_j - 2\lambda_j\bm{w}_j-\sum^{j-1}_{k=1}\mu_k\bm{w}_k &= 0\\ \end{align}$$

ここで、 $\bm{w}\_l\quad(l< j)$ を左から掛けると

$$\begin{align*} 2\bm{w}_l^TS\bm{w}_j - 2\lambda_j\bm{w}_l^T\bm{w}_j-\sum^{j-1}_{k=1}\mu_k\bm{w}_l^T\bm{w}_k &= 0\\ 2\bm{w}_l^TS\bm{w}_j -\mu_l&=0\\ \mu_l&=2\bm{w}_l^TS\bm{w}_j\\ \end{align*}$$

$S$ が対称行列であることと、前提条件を利用すると

$$\begin{align*} \mu_l&=2(\bm{w}_l^TS\bm{w}_j)^T\\ &=2\bm{w}_j^TS\bm{w}_l\\ &=2\bm{w}_j^T\lambda_l\bm{w}_l\\ &=2\lambda_l\bm{w}_j^T\bm{w}_l\\ &=0 \end{align*}$$

とラグランジュ乗数 $\mu_l$ は $0$ となり、式（1）は次のようになる

$$\begin{align*} 2S\bm{w}_j - 2\lambda_j\bm{w}_j &= 0\\ S\bm{w}_j - \lambda_j\bm{w}_j &= 0\\ S\bm{w}_j &= \lambda_j\bm{w}_j \end{align*}$$

つまり、第二主成分以降は制約条件が増えますが結局は第一主成分と同様に観測データの分散共分散行列の固有値・固有ベクトル問題となります。そして、左から $\bm{w}\_j$ を掛けると

$$\begin{align*} \bm{w}_j^TS\bm{w}_j &= \lambda_j\bm{w}_j^T\bm{w}_j\\ J_j &= \lambda_j \end{align*}$$

となり、分散と固有値が一致します。また前提条件より、第 $j-1$ 主成分まで求まっているので、第 $j$ 主成分の軸は $j$ 番目に大きい固有値に対応する固有ベクトルとなります。

寄与率と累積寄与率

主成分がどれだけデータの特徴を表現できているかを表す指標として寄与率と累積寄与率があります。どのように求めるかというと、分散を利用します。主成分得点（射影した後の点）の分散の和は

$$\begin{align*} \sum^{p}_{j=1}J_j &= \sum^{p}_{j=1}\lambda_j\\ &= tr(S) \end{align*}$$

ポイント $n$ 次正方行列 $A$ の固有値を重複しているものは別物として見なし、 $\lambda_1,\cdots,\lambda_p$ とすると

$$\begin{align*} tr(A) = \sum^{p}_{j=1}\lambda_j \end{align*}$$

すなわち、観測データの分散の総和と主成分の分散の総和は等しくなります。そこで、第 $j$ 主成分がどれだけ、観測データの特徴を表しているかを、第 $1$ から第 $p$ 主成分の分散の和に占める割合で表現します。これを寄与率といい、第 $j$ 主成分の寄与率は次のように定義されます。

寄与率

$$\begin{align*} \frac{\lambda_j}{\sum^{p}_{k=1}\lambda_k} = \frac{\lambda_j}{tr(S)} \end{align*}$$

そして、累積寄与率とは、第 $j$ 主成分までの寄与率の和です。

累積寄与率

$$\begin{align*} \frac{\sum^{j}_{l=1}\lambda_l}{\sum^{p}_{k=1}\lambda_k} = \frac{\sum^{j}_{l=1}\lambda_l}{tr(S)} \end{align*}$$

次元削減として主成分分析が用いられる場合、必ずではありませんが、この累積寄与率が $80\%$ を超える主成分までを選択することが多いです。

今回はここまでにしようと思います。かなりボリュームのある記事となりましたが、ここまで読んでいただけて幸いです。